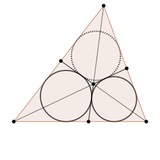
Forwarded from Геометрия-канал (knamprihodilinoneseichas knamprihodilinoneseichas)
Моя с Вовой Конышевым задача с 1 дня майский сборов.
Дан вписанный четырехугольник ABCD. Докажите, что существует окружность, касающаяся следующих пяти окружностей: описанной окружности четырехугольника ABCD, вписанных окружностей треугольников ABC и ABD, C-вневписанной окружности треугольника ACD и
D-вневписанной окружности треугольника BCD.
Дан вписанный четырехугольник ABCD. Докажите, что существует окружность, касающаяся следующих пяти окружностей: описанной окружности четырехугольника ABCD, вписанных окружностей треугольников ABC и ABD, C-вневписанной окружности треугольника ACD и
D-вневписанной окружности треугольника BCD.
Правильное условие и картинка
Пусть ABCD — вписанный четырёхугольник, O — точка пересечения диагоналей AC и BD. Пусть окружности, описанные около треугольников ABO и COD, пересекаются в точке K. Точка L такова, что треугольник BLC подобен треугольнику AKD. Докажите, что если четырёхугольник BLCK выпуклый, то он он является описанным.
Пусть ABCD — вписанный четырёхугольник, O — точка пересечения диагоналей AC и BD. Пусть окружности, описанные около треугольников ABO и COD, пересекаются в точке K. Точка L такова, что треугольник BLC подобен треугольнику AKD. Докажите, что если четырёхугольник BLCK выпуклый, то он он является описанным.
Всем привет! К сожалению с чатом, привязанным к этому каналу не очень дальше получается. Будем считать, что это был неудачный эксперимент.
К счастью теперь есть много других геометрических групп, почти у все этих групп есть чаты - там вы всегда найдете с кем обсудить что-то геометрическое.
К счастью теперь есть много других геометрических групп, почти у все этих групп есть чаты - там вы всегда найдете с кем обсудить что-то геометрическое.
Forwarded from Pavel Kozhevnikov
Часто ситуации, когда прямые можно "искривлять"
в коники, сохраняя дважды касание,
объясняются таким соображением:
Лемма (пучок, дважды касающемя сокружности в данных точках,
или обобщенная директриса для окружности и прямой).
Пусть коника $\omega = 0$ пересекает прямую $l=0$ в точках $A$ и $B$. Тогда коники, касающиеся $\omega = 0$ в точках $A$ и $B$ --- это пучок $\omega + \lambda l^2 = 0$.
(если $\omega$ --- окружность, то тут написано гмт $X$, для которых отношение $pow (X, \omega)$ к расстоянию от $X$ до $l$ равно const )
=========
Из этого утверждение следует в одну строчку:
Скажем, у нас пересекаются эллипсы $\omega + \lambda_1 l_1^2 = 0$ и
$\omega + \lambda_2 l_2^2 = 0$. Через точки их пересечения проходит вырожденная коника (пара прямых) $\lambda_1 l_1^2 - \lambda_2 l_1^2 = 0= 0$, которая, очевидно, проходит через
точку пересечения прямых $l_1=0$ и $l_2=0$.
=============
Еще о применении этого - напр. в последнем упражнении 17 статьи
https://www.mathnet.ru/links/be697473b64d836385257c3b19ae4332/kvant4535.pdf
============
Еще и еще ... - например, быстро решается задача Ф. Нилова
о параболическом 4-угольнике
https://www.mathnet.ru/links/c637ed850ac5245f76ddfe68fb2d9b99/mp254.pdf
Так:
Пусть $\omega = x^2+y^2-1$.
То, что $\omega - l_1^2 = 0$ --- параболического типа, задается условием $a_1^2+b^1=1$, где $l_1 = a_1x+b_1y+c_1$.
Аналогично для $l_2$. И отсюда получаем, что наша вырожденная коника (= пара диагоналей параболического 4-ка) $l_1^2-l_2^2 = 0$ --- это пара ортогональных прямых.
в коники, сохраняя дважды касание,
объясняются таким соображением:
или обобщенная директриса для окружности и прямой).
Пусть коника $\omega = 0$ пересекает прямую $l=0$ в точках $A$ и $B$. Тогда коники, касающиеся $\omega = 0$ в точках $A$ и $B$ --- это пучок $\omega + \lambda l^2 = 0$.
(если $\omega$ --- окружность, то тут написано гмт $X$, для которых отношение $pow (X, \omega)$ к расстоянию от $X$ до $l$ равно const )
=========
Из этого утверждение следует в одну строчку:
$\omega + \lambda_2 l_2^2 = 0$. Через точки их пересечения проходит вырожденная коника (пара прямых) $\lambda_1 l_1^2 - \lambda_2 l_1^2 = 0= 0$, которая, очевидно, проходит через
точку пересечения прямых $l_1=0$ и $l_2=0$.
=============
Еще о применении этого - напр. в последнем упражнении 17 статьи
https://www.mathnet.ru/links/be697473b64d836385257c3b19ae4332/kvant4535.pdf
============
Еще и еще ... - например, быстро решается задача Ф. Нилова
о параболическом 4-угольнике
https://www.mathnet.ru/links/c637ed850ac5245f76ddfe68fb2d9b99/mp254.pdf
Так:
То, что $\omega - l_1^2 = 0$ --- параболического типа, задается условием $a_1^2+b^1=1$, где $l_1 = a_1x+b_1y+c_1$.
Аналогично для $l_2$. И отсюда получаем, что наша вырожденная коника (= пара диагоналей параболического 4-ка) $l_1^2-l_2^2 = 0$ --- это пара ортогональных прямых.
This media is not supported in your browser
VIEW IN TELEGRAM
теорема о шести окружностях
Про треугольную цепочку из шести окружностей можно прочитать в статье из Математического просвещения
"Теорема о семи окружностях и другие новые теоремы"
"Теорема о семи окружностях и другие новые теоремы"
Докажите, что если два прямоугольных параллелепипеда имеют равные объёмы, то их можно расположить в пространстве так, что любая горизонтальная плоскость, пересекающая один из них, будет пересекать и второй, причём по многоугольнику той же площади.
ВсОШ-1993, 11.8. Автор: Терешин Д.А.
ВсОШ-1993, 11.8. Автор: Терешин Д.А.
Forwarded from Математические кружки | «МТ кружки»
🚀 МТ кружки теперь и на Дальнем Востоке!
Мы запускаем МТ кружки «Дальний Восток» для учеников 4–7 классов из Приморского, Хабаровского краев и соседних регионов. Теперь ребята из дальневосточных регионов смогут комфортно заниматься олимпиадной математикой в удобное время и по сильной авторской программе.
Эти кружки мы организуем совместно с замечательным преподавателем и методистом — Марией Дмитриевной Мониной, руководителем математических кружков Хабаровска.
🔸 Мария Дмитриевна Монина — кандидат физико-математических наук, победитель фонда «Династия» (2011, 2012) в номинации «Молодой учитель», преподаватель декабрьских смен Образовательного центра «Сириус», член жюри регионального этапа ВсОШ по математике в Хабаровском крае, руководитель краевых математических смен «МатКод».
📚 Что получают ученики:
— Регулярные онлайн-занятия в небольших группах
— Интерактивная платформа с задачами
— Возможность получать поддержку тьютора
— Подходит и для начинающих, и для уже опытных ребят
✨ Стоимость: от 1475 ₽ / 15 € в неделю
Мы хотим поддержать ребят из дальневосточных регионов и дать им возможность развиваться в олимпиадной математике наравне со школьниками центральных регионов страны.
📌 Подробнее на нашем сайте
✍️ Записаться на занятия
Мы запускаем МТ кружки «Дальний Восток» для учеников 4–7 классов из Приморского, Хабаровского краев и соседних регионов. Теперь ребята из дальневосточных регионов смогут комфортно заниматься олимпиадной математикой в удобное время и по сильной авторской программе.
Эти кружки мы организуем совместно с замечательным преподавателем и методистом — Марией Дмитриевной Мониной, руководителем математических кружков Хабаровска.
🔸 Мария Дмитриевна Монина — кандидат физико-математических наук, победитель фонда «Династия» (2011, 2012) в номинации «Молодой учитель», преподаватель декабрьских смен Образовательного центра «Сириус», член жюри регионального этапа ВсОШ по математике в Хабаровском крае, руководитель краевых математических смен «МатКод».
📚 Что получают ученики:
— Регулярные онлайн-занятия в небольших группах
— Интерактивная платформа с задачами
— Возможность получать поддержку тьютора
— Подходит и для начинающих, и для уже опытных ребят
✨ Стоимость: от 1475 ₽ / 15 € в неделю
Мы хотим поддержать ребят из дальневосточных регионов и дать им возможность развиваться в олимпиадной математике наравне со школьниками центральных регионов страны.
📌 Подробнее на нашем сайте
✍️ Записаться на занятия
This media is not supported in your browser
VIEW IN TELEGRAM
радикальная ось двух окружностей проходит через фиксированную точку
В последний день весны Олимпиадная геометрия объявляет конкурс на стипендию для обучения в математическом кружке на ваш выбор в первом полугодии 2025/2026 учебного года (сентябрь — декабрь).
Размер стипендий:
• 🥇 1 место — 100% покрытия стоимости обучения
• 🥈 2 место — 70%
• 🥉 3 место — 30%
К участию приглашаются школьники, которые:
• уже начали изучать геометрию,
• не обучаются в выпускном классе (по российской системе — 8, 9 или 10 класс),
• хотят заниматься в действующем математическом кружке, у которого:
— есть открытая страница в интернете (сайт, соцсеть или телеграм-канал),
— кружок основан не в этом году,
— указан список преподавателей и понятная система оплаты (цены указаны, есть контакт для связи).
Для участия необходимо до 15 июля 2025 года отправить письмо на [email protected]
Тема письма: [Фамилия Имя, город, класс]
Письмо должно содержать:
• Краткую информацию о себе: кто вы, в какой стране, городе и школе учитесь. (Можно указать достижения в математических соревнованиях но это не будет являться решающим фактором.)
• Мотивационное письмо — почему вам нужна стипендия.
• PDF-файл с тремя любимыми задачами по геометрии и их решениями. Не забудьте написать, почему вам нравятся эти задачи!
• Контактные данные преподавателей математики, которые могут вас порекомендовать (не забудьте заручиться их согласием). Сами рекомендательные письма присылать не нужно!
Важно:
Отправляя заявку, вы соглашаетесь, что в случае получения стипендии ваше имя может быть опубликовано в социальных сетях проекта Олимпиадная геометрия.
Подведение итогов: не позднее 15 августа
Размер стипендий:
• 🥇 1 место — 100% покрытия стоимости обучения
• 🥈 2 место — 70%
• 🥉 3 место — 30%
К участию приглашаются школьники, которые:
• уже начали изучать геометрию,
• не обучаются в выпускном классе (по российской системе — 8, 9 или 10 класс),
• хотят заниматься в действующем математическом кружке, у которого:
— есть открытая страница в интернете (сайт, соцсеть или телеграм-канал),
— кружок основан не в этом году,
— указан список преподавателей и понятная система оплаты (цены указаны, есть контакт для связи).
Для участия необходимо до 15 июля 2025 года отправить письмо на [email protected]
Тема письма: [Фамилия Имя, город, класс]
Письмо должно содержать:
• Краткую информацию о себе: кто вы, в какой стране, городе и школе учитесь. (Можно указать достижения в математических соревнованиях но это не будет являться решающим фактором.)
• Мотивационное письмо — почему вам нужна стипендия.
• PDF-файл с тремя любимыми задачами по геометрии и их решениями. Не забудьте написать, почему вам нравятся эти задачи!
• Контактные данные преподавателей математики, которые могут вас порекомендовать (не забудьте заручиться их согласием). Сами рекомендательные письма присылать не нужно!
Важно:
Отправляя заявку, вы соглашаетесь, что в случае получения стипендии ваше имя может быть опубликовано в социальных сетях проекта Олимпиадная геометрия.
Подведение итогов: не позднее 15 августа
На адрес Олимпиадной геометрии поступило несколько писем в формате "Хочу участвовать в конкурсе!" Поэтому, видимо, требуются некоторые пояснения.
Для участия в конкурсе надо отправить ОДНО письмо, содержащее всю необходимую информацию:
1) информацию о кандидате
2) мотивационное письмо
3) работу про три геометрические задачи
4) информация о кружке
5) контакты преподавателей, которые могут дать рекомендацию
Кроме того, пришло несколько писем с вопросами. Попробую на них ответить.
1. Мы оплачиваем кружок с использованием материнского капитала. Можно ли получить стипендию напрямую?
Нет. Стипендия будет переведена напрямую в кружок. Можете сэкономить материнский капитал на что-то другое.
2. Я не из России. Могу ли я участвовать?
Можете, ограничений нет. Более того, если комфортнее, можете выполнять работу на английском языке.
3. Могу ли я получить стипендию на кружок не в России?
Да, можете, если выполняются все требования к кружку (наличие доступной публичной информации о кружке и системе оплаты)
4. Я хотел бы заниматься в кружке, но не знаю возьмут ли меня. Что мне делать?
Укажите, в каком кружке вы хотели бы заниматься и постарайтесь узнать, возьмут ли вас до подведения итогов конкурса. В случае невозможности это сделать, укажите в письме, когда информация о зачислении в кружок станет известна.
5. Можно ли стипендию потратить на занятия математикой не в кружке?
Предпочтения будут отдаваться именно кружкам по олимпиадной математике.
Для участия в конкурсе надо отправить ОДНО письмо, содержащее всю необходимую информацию:
1) информацию о кандидате
2) мотивационное письмо
3) работу про три геометрические задачи
4) информация о кружке
5) контакты преподавателей, которые могут дать рекомендацию
Кроме того, пришло несколько писем с вопросами. Попробую на них ответить.
1. Мы оплачиваем кружок с использованием материнского капитала. Можно ли получить стипендию напрямую?
Нет. Стипендия будет переведена напрямую в кружок. Можете сэкономить материнский капитал на что-то другое.
2. Я не из России. Могу ли я участвовать?
Можете, ограничений нет. Более того, если комфортнее, можете выполнять работу на английском языке.
3. Могу ли я получить стипендию на кружок не в России?
Да, можете, если выполняются все требования к кружку (наличие доступной публичной информации о кружке и системе оплаты)
4. Я хотел бы заниматься в кружке, но не знаю возьмут ли меня. Что мне делать?
Укажите, в каком кружке вы хотели бы заниматься и постарайтесь узнать, возьмут ли вас до подведения итогов конкурса. В случае невозможности это сделать, укажите в письме, когда информация о зачислении в кружок станет известна.
5. Можно ли стипендию потратить на занятия математикой не в кружке?
Предпочтения будут отдаваться именно кружкам по олимпиадной математике.
Forwarded from Geometry Ukraine (sydorenko)
О высоте и радиусах.pdf
708.8 KB
Нова стаття від Григорія Борисовича.