group-telegram.com/def_model_train/1060
Last Update:
- Здесь аналогичное наблюдение, что "Aha moment" (которое в статье про r1 преподносилось как доказательство emergent capability к рефлексии своего ответа) наблюдается и до обучения, особенно у моделей Qwen и особенно при высоких температурах
- При этом, в base models (без RL-дообучения) эти размышления большую часть времени не приводят к правильному ответу или исправляют ответ на неправильный в ходе решения (это оценивали по Qwen2.5-Math-1.5B, но хотелось бы увидеть и модель побольше если честно)
- Еще одно наблюдение про связь длины ответа и reasoning capabilities: в своем эксперименте с возспроизведением тренировки r1 авторы показываеют, что на начальных шагах обучения модель больше всего выбивает реворд из следования формату, так как это выучить проще всего. В течение этой стадии, средняя длина ответа падает. Дальше модель начинает пытаться получать более высокий реворд за счет правильных ответов. Здесь длина генераций начинает расти, так как модель предепринимает много попыток прийти к правильному решению за раз. Как побочный эффект появляются и superficial self-reflections, когда модель рассуждает долго, но к правильному ответу не приходит, из-за такого специфичного misalignment. Получается, что все правильные ответы достигаются при длинных рассуждениях, и модель учится генерировать много, но не обязательно правильно
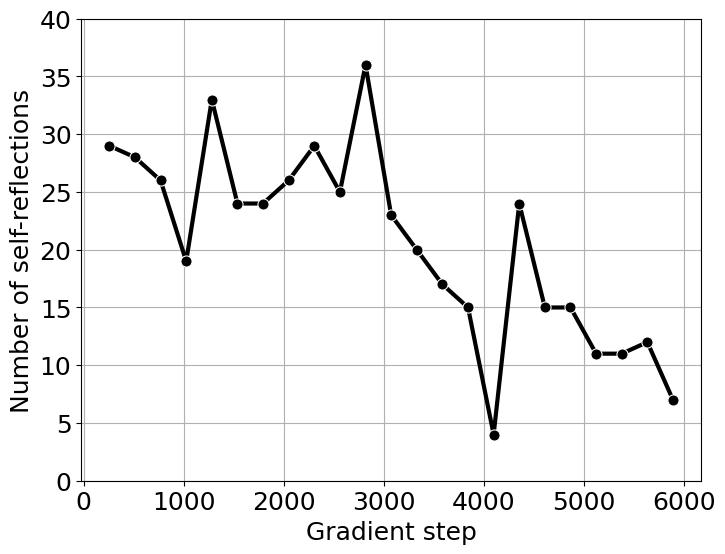
- При этом, дополнительно авторы показывают, что с длиной ответа не растет число self-reflection keywords вроде "check again", "let's verify" и так далее. До есть длина ответа снова получается не гарант того, что модель чему-то полезному научилась
Это как будто порождает еще больше новых вопросов касательно того, за счет чего скоры в ходе RL-тренировки продолжают расти, если увеличивается только длина, но не объем какой-то полезной саморефлексии. Может быть, наиболее правильные и выигрышные цепочки рассуждений просто требуют больше текста, даже если он не разбивается на большее число повторений "let's revisit our solution" и подобных? И можно ли найти тогда оптимальную длину ответа, при которой уже есть какое-от насыщение от ризонинга, и остановиться тогда на ней, вместо того, чтобы дальше скейлить число токенов?
Очень хорошая статья, тем более обожаю когда выводы в названии. Еще там необычные задачи для RL – карточная игра и визуальная задача по навигации по картам – обе из которых можно решить в pure language и vision-language формате
- SFT и для языковой, и для VLM модели лучше себя показывает, когда нужно просто выучить правила какой-нибудь игры, но только RL оказывается способен генерализоваться достаточно, чтобы решать out of distribution вариации задачи
- Но при этом SFT очень нужен, если модель изначально плохо следует формату или инструкциям – тогда RL просто не заводится
- RL скейлится с числом verification steps на инференсе, что уже в принципе было понятно из тех же экспериментов NVIDIA с генерацией cuda kernels по кругу, добавляя фидбек от модели-критика в промпт. Но теперь на это есть целая академическая ссылка
Для меня эта статья объясняет немного успех SFT-файнтюна на reasoning traces в стиле s1, о котором я писала парой постов выше. Если стартовать с уже неплохой модели (Qwen) и трениться, как это обычно делают, на математике, то ожидаемо вырастут скоры на математическихх и кодерским бенчах, на которые сейчас все смотрят. Но вряд ли из этого получится модель класса o1 / r1 в целом