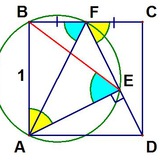
У задачи выше есть разные решения — например, такое:
Будем считать сторону квадрата равной 1. Если одна из сторон прямоугольника равна A, то его площадь не больше A (ведь вторая сторона не больше 1). Поэтому суммарна длина отмеченных отрезков не меньше суммарной площади всех прямоугольников, т.е. 1.
Задача, кстати, была на ММО и на Турнире городов, предложил ее В.В.Произволов.
Задача, кстати, была на ММО и на Турнире городов, предложил ее В.В.Произволов.
Telegram
Геометрия-канал
Квадрат разрезан на прямоугольники. В каждом прямоугольнике отмечена одна сторона. Доказать, что сумма длин отмеченных сторон не меньше стороны квадрата.
Предыдущее рассуждение учит, что квадрат нельзя закрыть планками, суммарная ширина которых меньше стороны квадрата, если каждую планку класть параллельно одной из сторон.
А если их разрешается класть как угодно? Оказывается, все равно планками суммарной ширины меньше 1 нельзя покрыть единичный квадрат… и даже единичный круг нельзя.
У этого утверждения есть замечательное геометрическое доказательство, опирающееся на лемму Архимеда. Можно прочитать его в статье А.Акопяна в Кванте — https://www.mathnet.ru/rus/kvant3725
А если их разрешается класть как угодно? Оказывается, все равно планками суммарной ширины меньше 1 нельзя покрыть единичный квадрат… и даже единичный круг нельзя.
У этого утверждения есть замечательное геометрическое доказательство, опирающееся на лемму Архимеда. Можно прочитать его в статье А.Акопяна в Кванте — https://www.mathnet.ru/rus/kvant3725
Forwarded from Геометрия с Ниловым
На квадратном торте расположены a) круглые; b) треугольные шоколадки, которые не соприкасаются между собой. Всегда ли можно разрезать торт на выпуклые многоугольники так, чтобы каждый многоугольник содержал ровно одну шоколадку? (Торт считайте плоским квадратом.)
P.S. Первый пункт взаимосвязан с областями Вороного, а второй пункт - задача А.Я. Канеля на тургоре
P.S. Первый пункт взаимосвязан с областями Вороного, а второй пункт - задача А.Я. Канеля на тургоре
Forwarded from Олимпиадная геометрия
Еще один шедевр от Георгия Галяпина и Станислава Кузнецова
Дан четырехугольник ABCD и точка P, не лежащая на описанных окружностях треугольников ABC, BCD, CDA и DAB. Пусть точки Pa, Pb, Pc и Pd} — изогонально сопряжены точке P относительно треугольников BCD, ACD, ABD и ABC соответственно. Оказалось, что прямые PaPc, AC и BD пересекаются в одной точке. Докажите, что через эту же точку проходит прямая PbPd.
Участники мне рассказали очень красивое решение, которое только добавляет этой задаче красоты (в дополнение к красивому решению, которое я и так знал).
Дан четырехугольник ABCD и точка P, не лежащая на описанных окружностях треугольников ABC, BCD, CDA и DAB. Пусть точки Pa, Pb, Pc и Pd} — изогонально сопряжены точке P относительно треугольников BCD, ACD, ABD и ABC соответственно. Оказалось, что прямые PaPc, AC и BD пересекаются в одной точке. Докажите, что через эту же точку проходит прямая PbPd.
Участники мне рассказали очень красивое решение, которое только добавляет этой задаче красоты (в дополнение к красивому решению, которое я и так знал).
Forwarded from Геометрия с Ниловым
Две окружности вписаны в эллипс. Тогда любая прямая, соединяющая точки касания эллипса с окружностями, высекает на этих окружностях равные хорды.
в «Олимпиадной геометрии» напомнили отличное утверждение
в прямоугольном треугольнике отметили точки касания (вне)вписанных окружностей со сторонами
доказать, что они лежат на двух окружностях
в прямоугольном треугольнике отметили точки касания (вне)вписанных окружностей со сторонами
доказать, что они лежат на двух окружностях
Forwarded from Олимпиадная геометрия
mp-32-cubics.pdf
874.6 KB
Кубические кривые
и элементарная геометрия (А.Заславский, П.Кожевников; МатПросвещение, сер. 3, вып. 32)
тут неоднократно спрашивали, где можно прочитать про использование сложения точек на кубиках и т.п. в планиметрии — ну так вот
остальные материалы выпуска, кстати, тоже доступны — см. https://mccme.ru/free-books/matpros/pdf/mp-32.pdf
и элементарная геометрия (А.Заславский, П.Кожевников; МатПросвещение, сер. 3, вып. 32)
тут неоднократно спрашивали, где можно прочитать про использование сложения точек на кубиках и т.п. в планиметрии — ну так вот
остальные материалы выпуска, кстати, тоже доступны — см. https://mccme.ru/free-books/matpros/pdf/mp-32.pdf
Forwarded from Pavel Kozhevnikov
Если что, вот версия, https://drive.google.com/file/d/1kKmd1Q0P1u6R2KLdKQghcQjxq_Zuq1Mt/view?usp=sharing с комментами - опечатки, баги, дополнения. В частности, очень порадовался, когда получил трактовку через кубики утверждения: Точка Микеля 4-сторонника лежит на окружности 9 точек
треугольника, образованного его диагоналями.
треугольника, образованного его диагоналями.
Forwarded from tropical saint petersburg
В детстве такие штуки глупостями казались, а сейчас, наоборот, испытываю эстетическое наслаждение.
Доказывается такой факт, если a^2=2b^2 то 2(a-b)^2=(2b-a)^2.Можно скобки раскрыть, а можно увидеть на первой картинке из соображений площадей.
На второй картинке катеты равны q, а гипотенуза p. Проведём из острого угла биссектрису, по ней сложим, и сверху получим прямоугольный треугольник с катетами p-q и гипотенузой 2q-p, что и требовалось.
Удовольствие платонического толка — смотришь, и практически осязаешь платоническую идею, оперируешь не формулами и силлогизмами, а воображаемыми листами бумаги.
Так можно доказать иррациональность корня из 2. От противного: если он рационален и равен a/b, то a^2=2b^2, а как показывают рассуждения выше, у такого уравнения нет наименьшего натурального решения (по каждому решению (a,b), a>b, можно построить решение (2b-a,a-b), и оно меньше).
Почему это в детстве не нравилось? потому что показывают фокус вместо технологии (и разводят глубокую философию на мелких местах).
Доказывается такой факт, если a^2=2b^2 то 2(a-b)^2=(2b-a)^2.
На второй картинке катеты равны q, а гипотенуза p. Проведём из острого угла биссектрису, по ней сложим, и сверху получим прямоугольный треугольник с катетами p-q и гипотенузой 2q-p, что и требовалось.
Удовольствие платонического толка — смотришь, и практически осязаешь платоническую идею, оперируешь не формулами и силлогизмами, а воображаемыми листами бумаги.
Так можно доказать иррациональность корня из 2. От противного: если он рационален и равен a/b, то a^2=2b^2, а как показывают рассуждения выше, у такого уравнения нет наименьшего натурального решения (по каждому решению (a,b), a>b, можно построить решение (2b-a,a-b), и оно меньше).
Почему это в детстве не нравилось? потому что показывают фокус вместо технологии (и разводят глубокую философию на мелких местах).
Очень красивая задача с командной олимпиады сеньоров с Колма, который идет прямо сейчас.
Биссектрисы AA1, BB1, CC1 неравнобедренного треугольника ABC пересекаются в точке I. Впи-
санная окружность треугольника ABC касается стороны BC в точке A2. Окружность ωa проходит
через точки A1, A2 и середину отрезка AI. Окружности ωb и ωc определяются аналогично. Докажите,
что центры окружностей ωa, ωb, ωc лежат на одной прямой.
Биссектрисы AA1, BB1, CC1 неравнобедренного треугольника ABC пересекаются в точке I. Впи-
санная окружность треугольника ABC касается стороны BC в точке A2. Окружность ωa проходит
через точки A1, A2 и середину отрезка AI. Окружности ωb и ωc определяются аналогично. Докажите,
что центры окружностей ωa, ωb, ωc лежат на одной прямой.
Forwarded from Фулл и точка
This media is not supported in your browser
VIEW IN TELEGRAM
#колм
Публикуем задачи первого тура кубка Колмогорова. Обсудить их вы можете в комментариях👇
Задача. Внутри остроугольного треугольника 𝐴𝐵𝐶, в котором ∠𝐴 = 60°, выбирается переменная точка 𝑃 так, что ∠𝐵𝑃𝐶 = 120°. Точки 𝑃₂, 𝑃₃ симметричны точке 𝑃 относительно сторон 𝐴𝐶, 𝐴𝐵 соответственно. Прямые 𝐵𝑃₂ , 𝐶𝑃₃ пересекаются в точке 𝑄. Докажите, что описанная окружность треугольника 𝐴𝑃𝑄 проходит через точку, отличную от 𝐴 и не зависящую от выбора 𝑃 .
Публикуем задачи первого тура кубка Колмогорова. Обсудить их вы можете в комментариях👇
Задача. Внутри остроугольного треугольника 𝐴𝐵𝐶, в котором ∠𝐴 = 60°, выбирается переменная точка 𝑃 так, что ∠𝐵𝑃𝐶 = 120°. Точки 𝑃₂, 𝑃₃ симметричны точке 𝑃 относительно сторон 𝐴𝐶, 𝐴𝐵 соответственно. Прямые 𝐵𝑃₂ , 𝐶𝑃₃ пересекаются в точке 𝑄. Докажите, что описанная окружность треугольника 𝐴𝑃𝑄 проходит через точку, отличную от 𝐴 и не зависящую от выбора 𝑃 .
Еще одна задача с колма. Без картинки.
Дан вписанный пятиугольник P1P2P3P4P5; положим P6 = P1 и P0 = P5. При k = 1, 2, 3, 4, 5
обозначим через Ik центр вписанной окружности треугольника Pk−1PkPk+1. Оказалось, что пяти-
угольник I1I2I3I4I5 также является вписанным. Докажите, что прямые P1I1, P2I2, P3I3, P4I4 и P5I5
пересекаются в одной точке.
Дан вписанный пятиугольник P1P2P3P4P5; положим P6 = P1 и P0 = P5. При k = 1, 2, 3, 4, 5
обозначим через Ik центр вписанной окружности треугольника Pk−1PkPk+1. Оказалось, что пяти-
угольник I1I2I3I4I5 также является вписанным. Докажите, что прямые P1I1, P2I2, P3I3, P4I4 и P5I5
пересекаются в одной точке.
Forwarded from Фулл и точка
#колм
Сегодня на кубке Колмогорова 🏆 прошли вторые туры матбоев. Присоединяйтесь к обсуждению матчей и задач в комментариях👇
Задача. Точки 𝐻 и 𝑂 – ортоцентр и центр описанной окружности остроугольного неравнобедренного треугольника 𝐴𝐵𝐶 соответственно. Точки 𝑃 и 𝑄 выбраны на описанной окружности 𝜔 так, что ∠𝐵𝑃𝐻 = ∠𝐶𝑄𝐻 = 90°. Пусть прямая 𝑃𝑄 пересекает касательную к 𝜔, проведенную в точке 𝐴, в точке 𝑆, а отрезки 𝑂𝑃 и 𝑂𝑄 пересекают отрезки 𝐵𝐻 и 𝐶𝐻 в точках 𝑋 и 𝑌 соответственно. Докажите, что 𝑂𝑆 ‖ 𝑋𝑌.
Сегодня на кубке Колмогорова 🏆 прошли вторые туры матбоев. Присоединяйтесь к обсуждению матчей и задач в комментариях👇
Задача. Точки 𝐻 и 𝑂 – ортоцентр и центр описанной окружности остроугольного неравнобедренного треугольника 𝐴𝐵𝐶 соответственно. Точки 𝑃 и 𝑄 выбраны на описанной окружности 𝜔 так, что ∠𝐵𝑃𝐻 = ∠𝐶𝑄𝐻 = 90°. Пусть прямая 𝑃𝑄 пересекает касательную к 𝜔, проведенную в точке 𝐴, в точке 𝑆, а отрезки 𝑂𝑃 и 𝑂𝑄 пересекают отрезки 𝐵𝐻 и 𝐶𝐻 в точках 𝑋 и 𝑌 соответственно. Докажите, что 𝑂𝑆 ‖ 𝑋𝑌.
Forwarded from Фулл и точка
#колм #красота_спасет_мир
Подошел к концу третий день турнира Колмогорова, и мы, как обычно, радуем вас задачами с него 💥
Задача. На сторонах 𝐵𝐶, 𝐶𝐴 и 𝐴𝐵 треугольника 𝐴𝐵𝐶 выбраны точки 𝐴₁, 𝐵₁ и 𝐶₁ соответственно. Четырёхугольники 𝐴𝐵₁𝐴₁𝐶₁, 𝐵𝐶₁𝐵₁𝐴₁ и 𝐶𝐴₁𝐶₁𝐵₁ описаны около окружностей с центрами 𝐼𝑎, 𝐼𝑏 и 𝐼𝑐 соответственно. Докажите, что площади треугольников 𝐴₁𝐵₁𝐶₁ и 𝐼𝑎𝐼𝑏𝐼𝑐 отличаются в четыре раза.
Подошел к концу третий день турнира Колмогорова, и мы, как обычно, радуем вас задачами с него 💥
Задача. На сторонах 𝐵𝐶, 𝐶𝐴 и 𝐴𝐵 треугольника 𝐴𝐵𝐶 выбраны точки 𝐴₁, 𝐵₁ и 𝐶₁ соответственно. Четырёхугольники 𝐴𝐵₁𝐴₁𝐶₁, 𝐵𝐶₁𝐵₁𝐴₁ и 𝐶𝐴₁𝐶₁𝐵₁ описаны около окружностей с центрами 𝐼𝑎, 𝐼𝑏 и 𝐼𝑐 соответственно. Докажите, что площади треугольников 𝐴₁𝐵₁𝐶₁ и 𝐼𝑎𝐼𝑏𝐼𝑐 отличаются в четыре раза.