Проекциями некоторого треугольника на каждую из двух перпендикулярных плоскостей являются а) правильные; б) равнобедренные прямоугольные треугольники. Могут ли они быть неравными?
// А.Д.Блинков рассказал задачу
// А.Д.Блинков рассказал задачу
👍2🔥1
Forwarded from Геометрия с Ниловым
Приятная геометрия с сегодняшнего устного тура Турнира Городов.
На плоскости расположены круг и правильный 100-угольник, имеющие одинаковые площади. Какое наибольшее число вершин 100-угольника могут находиться внутри круга?
Любопытно дополнительно подумать, можно ли что-то разумное в трехмерном пространстве спросить по аналогии?
На плоскости расположены круг и правильный 100-угольник, имеющие одинаковые площади. Какое наибольшее число вершин 100-угольника могут находиться внутри круга?
Любопытно дополнительно подумать, можно ли что-то разумное в трехмерном пространстве спросить по аналогии?
❤9🔥3👍1
Forwarded from Геометрия с Ниловым
Теорема Сильвестра-Галлаи утверждает, что для любого конечного числа точек на плоскости, не лежащих на одной прямой, существует прямая, проходящая ровно через две точки данного множества.
Разумно сформулировать аналогичный вопрос для пространства:
Верно ли, что для любого конечного числа точек в пространстве, не лежащих в одной плоскости, существует плоскость, проходящая ровно через три неколлинеарные точки данного множества?
Интересно, что ответ здесь отрицательный. Попробуйте придумать какие-то контр-примеры.
Разумно сформулировать аналогичный вопрос для пространства:
Верно ли, что для любого конечного числа точек в пространстве, не лежащих в одной плоскости, существует плоскость, проходящая ровно через три неколлинеарные точки данного множества?
Интересно, что ответ здесь отрицательный. Попробуйте придумать какие-то контр-примеры.
❤9🤔6👍1👎1
Задача 8 из олимпиады 239, которая прошла недавно. Предлагалась для 8-9 класса. Остальные задачи можно найти тут.
Вписанная окружность прямоугольного треугольника ABC касается его гипотенузы BC в точке D. Прямая AD пересекает описанную окружность в точке X.
Докажите, что |BX − CX| ≥ |AD − DX|.
Вписанная окружность прямоугольного треугольника ABC касается его гипотенузы BC в точке D. Прямая AD пересекает описанную окружность в точке X.
Докажите, что |BX − CX| ≥ |AD − DX|.
❤8😱2
Forwarded from Геометрия от Волчкевича
Треугольник с углами 40, 60 и 80 градусов.
Пожалуй самую красивую задачу, которую я придумал за последний год, вчера решали семиклассники на Московской устной олимпиаде. Само собой, что она была быть им по возрасту, то есть должна иметь решение без счета и тригонометрии. Предлагаю вам над ней тоже подумать. Обещаю: получите большое удовольствие!
Пожалуй самую красивую задачу, которую я придумал за последний год, вчера решали семиклассники на Московской устной олимпиаде. Само собой, что она была быть им по возрасту, то есть должна иметь решение без счета и тригонометрии. Предлагаю вам над ней тоже подумать. Обещаю: получите большое удовольствие!
❤18
Геометрия-канал
синий треугольник вписан в параболу; касательные в его вершинах образуют зеленый треугольник — доказать, что его площадь вдвое меньше площади синего // задача M2831 из Кванта, предложил М.Панов
JMO 2017.
Дан правильный треугольник ABC и точка P на его описанной окружности. Прямые AP,BP,CP пересекают прямые BC,AC,AB в точках D,E,F соответственно. Докажите, что площадь DEF в два раза больше, чем у ABC.
Попробуйте понять связь c этой задачей)
Дан правильный треугольник ABC и точка P на его описанной окружности. Прямые AP,BP,CP пересекают прямые BC,AC,AB в точках D,E,F соответственно. Докажите, что площадь DEF в два раза больше, чем у ABC.
Попробуйте понять связь c этой задачей)
👍2❤1
Forwarded from Записки юного геометра на пенсии (Щербатов Ярослав)
Немного проспал(буквально) конец олимпиады, но вот моя задача с сегодняшней олимпиады. По-моему очень презабавно утверждение как факт...
Московская устная олимпиада по геометрии, 2025 год, 10-11 класс, Задача 6.
Московская устная олимпиада по геометрии, 2025 год, 10-11 класс, Задача 6.
❤5👍3
на сайте устных олимпиад ( https://olympiads.mccme.ru/ustn/ ) кроме условий устной олимпиады по геометрии появились решения, списки победителей и призеров, статистика
❤5
Forwarded from Кроссворд Тьюринга (Vanya Yakovlev)
В этот раз выступит Валентина Кириченко — математик, профессор матфака ВШЭ. Это особенно приятно, потому что многие авторы «Кроссворда» учились у Валентины Алексеевны.
В начальной школе нас учат вычислять площади квадрата, прямоугольника и других простых фигур с прямолинейными границами.
Но как найти площадь фигуры, ограниченной кривыми линиями? Например, площадь круга или луночки? В старших классах обычно говорят про загадочное число пи, выписывают формулу «пи эр квадрат» и на этом ставят точку. Но на самом деле за числом пи стоит интересная древняя история, полная интеллектуальных взлётов и падений.
Первые достижения – это три луночки Гиппократа Хиосского, придуманные им примерно за пять веков до нашей эры. Мы поговорим об идеях Гиппократа и об их развитии от Древней Греции до наших дней.
Для понимания лекции полезно помнить, что такое треугольник, квадрат, круг и другие базовые геометрические фигуры, которые изучают в детском саду. Формулы для площади фигур помнить не обязательно.
#матклуб #анонс
Please open Telegram to view this post
VIEW IN TELEGRAM
👍13❤2
Forwarded from Квантландия | Интересные задачи и не только
Хорошая задача будит не только наш разум, но и наши эмоции.
В.В. Произволов
Мне снова встретилась отличная классическая задачка Вячеслава Викторовича Произволова. Хорошо подойдёт для эмблемы какой-нибудь математической олимпиады:)
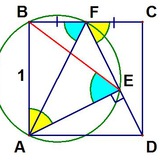
В квадрате построена четырёхзвенная ломаная так, что три угла равны 45 градусов, а одна из вершин совпадает с вершиной квадрата (см. рисунок). Докажите, что пять вершин этой ломаной лежат на одной окружности.
Изящный факт, не правда ли? Ставьте ❤️, если Вы со мной согласны.
#ГеометрияДляВсех
❤41👍9🔥4
Forwarded from Геометрия с Ниловым
1) Существует ли тетраэдр, основания высот которого не принадлежат граням?
2) Существует ли выпуклый многогранник и точка внутри такая, что основания всех перпендикуляров, опущенных из нее на грани, не принадлежат граням?
2) Существует ли выпуклый многогранник и точка внутри такая, что основания всех перпендикуляров, опущенных из нее на грани, не принадлежат граням?
🔥8
Forwarded from Кроссворд Тьюринга (Vanya Yakovlev)
Квадартура Луночки
По просьбам тех, кто был на пятничном рассказе Валентины Алексеевны на матклубе в Циферблате, выкладываем слайды.
Тем, кто не был, можно прочитать серию из двух статей в Квантике (начало и окончание) или публикацию на сайте Мел. Они очень хорошо написаны.
А еще на лекции была задача с картинки, можно попробовать с ней разобраться для разминки
По просьбам тех, кто был на пятничном рассказе Валентины Алексеевны на матклубе в Циферблате, выкладываем слайды.
Тем, кто не был, можно прочитать серию из двух статей в Квантике (начало и окончание) или публикацию на сайте Мел. Они очень хорошо написаны.
А еще на лекции была задача с картинки, можно попробовать с ней разобраться для разминки
🔥6❤3👍3
1) Дан параллелограмм ABCD. Точки E и F выбраны на сторонах AD и AB так, что BE = DF. Отрезки BE и CF пересекаются в точке G. Докажите, что C лежит на биссектрисе угла BGD.
2) Докажите теорему Штейнера — Лемуса (если в треугольнике равны 2 биссектрисы, то этот треугольник является равнобедренным)
2) Докажите теорему Штейнера — Лемуса (если в треугольнике равны 2 биссектрисы, то этот треугольник является равнобедренным)
😢20👍7🔥3❤2
Forwarded from Геометрия с Ниловым
На плоскости даны семейство красных и семейство синих прямых. Известно, что в каждом семействе нет параллельных прямых. Зафиксируем некоторый угол. Для каждой синей прямой выберем (в случае, если это возможно) красную прямую, пересекающую ее под данным ориентированным углом, и отметим точку пересечения. Оказалось, что для любого угла все точки пересечения красных и синих прямых (пересекающимися под данным углом) лежат на одной окружности. Как могут быть устроены семейства красных и синих прямых? Например, это могут быть два пучка прямых. Я знаю еще только два примера.
👎12👍3❤2🔥1🥰1