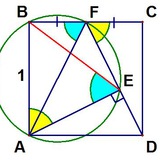
Задача 8 из олимпиады 239, которая прошла недавно. Предлагалась для 8-9 класса. Остальные задачи можно найти тут.
Вписанная окружность прямоугольного треугольника ABC касается его гипотенузы BC в точке D. Прямая AD пересекает описанную окружность в точке X.
Докажите, что |BX − CX| ≥ |AD − DX|.

синий треугольник вписан в параболу; касательные в его вершинах образуют зеленый треугольник — доказать, что его площадь вдвое меньше площади синего

// задача M2831 из Кванта, предложил М.Панов

Треугольник с углами 40, 60 и 80 градусов.

Пожалуй самую красивую задачу, которую я придумал за последний год, вчера решали семиклассники на Московской устной олимпиаде. Само собой, что она была быть им по возрасту, то есть должна иметь решение без счета и тригонометрии. Предлагаю вам над ней тоже подумать. Обещаю: получите большое удовольствие!

JMO 2017.
Дан правильный треугольник ABC и точка P на его описанной окружности. Прямые AP,BP,CP пересекают прямые BC,AC,AB в точках D,E,F соответственно. Докажите, что площадь DEF в два раза больше, чем у ABC.
Попробуйте понять связь c этой задачей)

Немного проспал(буквально) конец олимпиады, но вот моя задача с сегодняшней олимпиады. По-моему очень презабавно утверждение как факт...

Московская устная олимпиада по геометрии, 2025 год, 10-11 класс, Задача 6.

В пару окружностей вписывают треугольник ABC как показано на рисунке¹ всевозможными способами. Доказать, что все полученные так медианы AM проходят через одну точку.

¹ Т.е. A на одной окружности, B и C на другой, AB и AC проходят через P и Q.

на сайте устных олимпиад ( https://olympiads.mccme.ru/ustn/ ) кроме условий устной олимпиады по геометрии появились решения, списки победителей и призеров, статистика

Задача 9-10.8 с второго дня всеросса.
Красные чевианы равны между собой и равны черным.
Докажите, что периметры красного и черного треугольника равны.

1) Существует ли тетраэдр, основания высот которого не принадлежат граням?
2) Существует ли выпуклый многогранник и точка внутри такая, что основания всех перпендикуляров, опущенных из нее на грани, не принадлежат граням?

Квадартура Луночки

По просьбам тех, кто был на пятничном рассказе Валентины Алексеевны на матклубе в Циферблате, выкладываем слайды.

Тем, кто не был, можно прочитать серию из двух статей в Квантике (начало и окончание) или публикацию на сайте Мел. Они очень хорошо написаны.

А еще на лекции была задача с картинки, можно попробовать с ней разобраться для разминки

1) Дан параллелограмм ABCD. Точки E и F выбраны на сторонах AD и AB так, что BE = DF. Отрезки BE и CF пересекаются в точке G. Докажите, что C лежит на биссектрисе угла BGD.

2) Докажите теорему Штейнера — Лемуса (если в треугольнике равны 2 биссектрисы, то этот треугольник является равнобедренным)

На плоскости даны семейство красных и семейство синих прямых. Известно, что в каждом семействе нет параллельных прямых. Зафиксируем некоторый угол. Для каждой синей прямой выберем (в случае, если это возможно) красную прямую, пересекающую ее под данным ориентированным углом, и отметим точку пересечения. Оказалось, что для любого угла все точки пересечения красных и синих прямых (пересекающимися под данным углом) лежат на одной окружности. Как могут быть устроены семейства красных и синих прямых? Например, это могут быть два пучка прямых. Я знаю еще только два примера.

Добрая задача.
Дан параллелограмм ABCD с углом A = 60. Точка I — центр вписанной окружности треугольника ABD. Докажите, что BI + DI = CI.

Добрый день. Во вторник, 29 апреля в 15:30-16:30 по Москве, будет математический кружок 🟢

Title: Самозаклинивающиеся структуры

Speaker: Ф. K. Нилов

Аннотация:

Известно, что если на плоскости имеется конечный набор выпуклых фигур, внутренности которых не пересекаются, то среди этих фигур имеется хотя бы одна крайняя - такая, которую можно непрерывно передвинуть “на бесконечность” (за пределы большого круга, содержащего остальные фигуры), оставляя все остальные фигуры неподвижными и не пересекая их внутренности в процессе движения.

А что происходит в пространстве? На первый взгляд кажется, что должны быть справедливы аналогичные утверждения. Например, их можно доказать в частном случае, когда все тела являются шарами (для произвольной размерности). Однако в общем случае оказывается, что в пространстве имеет место феномен самозаклинивающихся структур. Самозаклинивающаяся структура — такой (конечный или бесконечный) набор выпуклых тел с непересекающимися внутренностями, что если зафиксировать все, кроме любого одного, оставшееся нельзя “унести на бесконечность”, не пересекая внутренности других тел в процессе движения.

Мы обсудим уже известные и новые стуктуры, построенные совсем недавно.


Zoom meeting link:
Zoom - Meeting ID: 853 1771 8785 Passcode: 549695
Link: https://us02web.zoom.us/j/85317718785?pwd=XS0bILZaREyt00pA2EJlu1zxaEHbDN.1

Приходите!

Номер 3 за 2025 год в продаже:
https://biblio.mccme.ru/node/286493

в Квант №3 вошла статья «Угол между радиусом и стороной» Ю.Блинкова и Д.Швецова