#геом_разминка
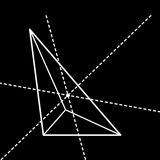
Задача. В выпуклом четырехугольнике 𝐴𝐵𝐶𝐷 углы ∠𝐴𝐵𝐶 и ∠𝐵𝐶𝐷 не меньше 120°. Докажите, что 𝐴𝐶 + 𝐵𝐷 > 𝐴𝐵 + 𝐵𝐶 + 𝐶𝐷.
Задача. В выпуклом четырехугольнике 𝐴𝐵𝐶𝐷 углы ∠𝐴𝐵𝐶 и ∠𝐵𝐶𝐷 не меньше 120°. Докажите, что 𝐴𝐶 + 𝐵𝐷 > 𝐴𝐵 + 𝐵𝐶 + 𝐶𝐷.
#геом_разминка
Задача. В параллелограмме 𝐴𝐵𝐶𝐷 точка 𝑀 — середина 𝐵𝐶, а точка 𝑁 — произвольная точка на стороне 𝐴𝐷. Пусть 𝑄 — пересечение 𝑀𝑁 и 𝐴𝐶, а 𝑃 — пересечение 𝐴𝑀 и 𝐵𝑁 . Докажите, что треугольники 𝐵𝐷𝑃 и 𝐷𝑀𝑄 имеют равные площади.
Задача. В параллелограмме 𝐴𝐵𝐶𝐷 точка 𝑀 — середина 𝐵𝐶, а точка 𝑁 — произвольная точка на стороне 𝐴𝐷. Пусть 𝑄 — пересечение 𝑀𝑁 и 𝐴𝐶, а 𝑃 — пересечение 𝐴𝑀 и 𝐵𝑁 . Докажите, что треугольники 𝐵𝐷𝑃 и 𝐷𝑀𝑄 имеют равные площади.
#геом_разминка
Задача. Пусть 𝑀 — середина боковой стороны 𝐴𝐵 трапеции 𝐴𝐵𝐶𝐷, 𝑂 — точка пересечения ее диагоналей, причем 𝐴𝑂 = 𝐵𝑂. На луче 𝑂𝑀 отмечена точка 𝑃 так, что ∠𝑃𝐴𝐶 = 90°. Докажите, что ∠𝐴𝑀𝐷 = ∠𝐴𝑃𝐶.
Задача. Пусть 𝑀 — середина боковой стороны 𝐴𝐵 трапеции 𝐴𝐵𝐶𝐷, 𝑂 — точка пересечения ее диагоналей, причем 𝐴𝑂 = 𝐵𝑂. На луче 𝑂𝑀 отмечена точка 𝑃 так, что ∠𝑃𝐴𝐶 = 90°. Докажите, что ∠𝐴𝑀𝐷 = ∠𝐴𝑃𝐶.
Игра в кальмара начинается!
Мы запускаем математико-психологический эксперимент 🧬 Не бойтесь 😨, никто не пострадает!
Правила просты:
У вас есть 100 монет. Какую-то часть из этих монет вы можете положить в красную 🔴 копилку, а какую-то в синию 🔵. При этом вы не знаете как кладут монеты в эти копилки другие игроки.
В конце игры мы разобьем обе копилки. И вернем вам все монеты 🪙 ровно столько сколько каждый положил.
Но если в синей копилке монет будет больше чем в два раза по сравнению с красной, то мы восстановим справедливость ⚖: и за каждую вашу монету из красной копилки доплатим еще по одной монете.
Цель 🎯: набрать как можно больше монет под конец игры.
Участовать можно просто перейдя в нашего ТГ-бота 👉 @bonka_game_bot 👈
Итоги 🏆 подведем уже завтра в 19:00 и заодно объясним, что к чему. Спешите принять участие!
Мы запускаем математико-психологический эксперимент 🧬 Не бойтесь 😨, никто не пострадает!
Правила просты:
У вас есть 100 монет. Какую-то часть из этих монет вы можете положить в красную 🔴 копилку, а какую-то в синию 🔵. При этом вы не знаете как кладут монеты в эти копилки другие игроки.
В конце игры мы разобьем обе копилки. И вернем вам все монеты 🪙 ровно столько сколько каждый положил.
Но если в синей копилке монет будет больше чем в два раза по сравнению с красной, то мы восстановим справедливость ⚖: и за каждую вашу монету из красной копилки доплатим еще по одной монете.
Цель 🎯: набрать как можно больше монет под конец игры.
Участовать можно просто перейдя в нашего ТГ-бота 👉 @bonka_game_bot 👈
Итоги 🏆 подведем уже завтра в 19:00 и заодно объясним, что к чему. Спешите принять участие!
#геом_разминка
Задача. Пусть 𝐴𝐵𝐶𝐷 — параллелограмм, диагонали которого пересекаются в точке 𝑃 . Обозначим через 𝑀 середину 𝐴𝐵. Пусть 𝑄 — точка, в которой 𝑄𝐴 касается окружности 𝑀𝐴𝐷, а 𝑄𝐵 касается окружности 𝑀𝐵𝐶. Докажите, что точки 𝑄, 𝑀, 𝑃 лежат на одной прямой.
Задача. Пусть 𝐴𝐵𝐶𝐷 — параллелограмм, диагонали которого пересекаются в точке 𝑃 . Обозначим через 𝑀 середину 𝐴𝐵. Пусть 𝑄 — точка, в которой 𝑄𝐴 касается окружности 𝑀𝐴𝐷, а 𝑄𝐵 касается окружности 𝑀𝐵𝐶. Докажите, что точки 𝑄, 𝑀, 𝑃 лежат на одной прямой.
Подводим итоги первой игры!
В игре приняло участие 135 игроков. На красных 🔴 суммарно поставлено 8193 монеты, на синих 🔵 — 5307.
Исходная игра вдохновлена дилеммой заключенного #️⃣ Здесь очевидно, что если каждый из игроков будет ставить 33 🔴 к 67 🔵, то все красные получат по дополнительной монете 🪙 и тем самым такая ставка при наличии между игроками предварительной договоренности приведет к наибольшему гарантированному всеобщему благу.
Однако, у подобной стратегии имеется дефект: на каждых три ставки вида 33 🔴 к 67 🔵 можно условно "безболезненно" для общего блага сделать ставку 34 🔴 к 66 🔵. Так что имеется вероятностная стратегия. Когда каждый из игроков подбрасывает ассимметричную монетку и с вероятностью 1/3 делает ставку 34 🔴 к 66 🔵 и с вероятностью 2/3 ставку 33 🔴 к 67 🔵.
Задача. Правда ли, что вероятностная стратегия в среднем эффективнее обычной?
Однако, все математические стратегии бьются о скалы реальности 🪨🌊 когда разговор заходит о нескоординированных действиях игроков.
Здесь равновесие ⚖️ наступает в невыгодном для всех положении из индивидуального желания получить как можно большую выгоду или же преднамеренной цели сорвать выигрыш остальным.
Будем, считать, что именно любопытство 🤔 и желание экспериментировать 🧑🔬 возобладали в наших читателях и сдвинули результат эксперимента настолько сильно в пользу красной команды
В игре приняло участие 135 игроков. На красных 🔴 суммарно поставлено 8193 монеты, на синих 🔵 — 5307.
Исходная игра вдохновлена дилеммой заключенного #️⃣ Здесь очевидно, что если каждый из игроков будет ставить 33 🔴 к 67 🔵, то все красные получат по дополнительной монете 🪙 и тем самым такая ставка при наличии между игроками предварительной договоренности приведет к наибольшему гарантированному всеобщему благу.
Однако, у подобной стратегии имеется дефект: на каждых три ставки вида 33 🔴 к 67 🔵 можно условно "безболезненно" для общего блага сделать ставку 34 🔴 к 66 🔵. Так что имеется вероятностная стратегия. Когда каждый из игроков подбрасывает ассимметричную монетку и с вероятностью 1/3 делает ставку 34 🔴 к 66 🔵 и с вероятностью 2/3 ставку 33 🔴 к 67 🔵.
Задача. Правда ли, что вероятностная стратегия в среднем эффективнее обычной?
Однако, все математические стратегии бьются о скалы реальности 🪨🌊 когда разговор заходит о нескоординированных действиях игроков.
Здесь равновесие ⚖️ наступает в невыгодном для всех положении из индивидуального желания получить как можно большую выгоду или же преднамеренной цели сорвать выигрыш остальным.
Будем, считать, что именно любопытство 🤔 и желание экспериментировать 🧑🔬 возобладали в наших читателях и сдвинули результат эксперимента настолько сильно в пользу красной команды
#разминка
Предлагаем вам задачку с заключительного этапа недавно прошедшей олимпиады Эйлера.
Задача. Дано натуральное число 𝑛. Докажите, что при некотором натуральном 𝑚 у числа 𝑚³ + 𝑚 ровно один или ровно два различных простых делителя, больших 𝑛.
Предлагаем вам задачку с заключительного этапа недавно прошедшей олимпиады Эйлера.
Задача. Дано натуральное число 𝑛. Докажите, что при некотором натуральном 𝑚 у числа 𝑚³ + 𝑚 ровно один или ровно два различных простых делителя, больших 𝑛.
#геом_разминка
Задача. Пусть 𝐴𝐵𝐶 — остроугольный треугольник, Ω — описанная около него окружность с диаметром 𝐴𝑃. Точки 𝐸 и 𝐹 — ортогональные проекции из 𝐵 на 𝐴𝐶 и 𝐴𝑃 , точки 𝑀 и 𝑁 — середины отрезков 𝐸𝐹 и 𝐶𝑃 . Докажите, что ∠𝐵𝑀𝑁 = 90°.
Задача. Пусть 𝐴𝐵𝐶 — остроугольный треугольник, Ω — описанная около него окружность с диаметром 𝐴𝑃. Точки 𝐸 и 𝐹 — ортогональные проекции из 𝐵 на 𝐴𝐶 и 𝐴𝑃 , точки 𝑀 и 𝑁 — середины отрезков 𝐸𝐹 и 𝐶𝑃 . Докажите, что ∠𝐵𝑀𝑁 = 90°.
#геом_разминка
Публикуем задачу 🐿 со вчерашнего второго тура ММО. Как прошло? Пишите в комментах 👇
Задача. Пусть 𝑂 — центр описанной окружности остроугольного треугольника 𝐴𝐵𝐶. На стороне 𝐵𝐶 отметили точку 𝐷. Окружности, описанные около треугольников 𝐵𝑂𝐷 и 𝐶𝑂𝐷, повторно пересекают отрезки 𝐴𝐵 и 𝐴𝐶 в точках 𝑋 и 𝑌 соответственно. Докажите, что из отрезков 𝐵𝑋, 𝑋𝑌 и 𝑌𝐶 можно сложить треугольник.
Публикуем задачу 🐿 со вчерашнего второго тура ММО. Как прошло? Пишите в комментах 👇
Задача. Пусть 𝑂 — центр описанной окружности остроугольного треугольника 𝐴𝐵𝐶. На стороне 𝐵𝐶 отметили точку 𝐷. Окружности, описанные около треугольников 𝐵𝑂𝐷 и 𝐶𝑂𝐷, повторно пересекают отрезки 𝐴𝐵 и 𝐴𝐶 в точках 𝑋 и 𝑌 соответственно. Докажите, что из отрезков 𝐵𝑋, 𝑋𝑌 и 𝑌𝐶 можно сложить треугольник.
#геом_разминка
Ловите задачку со вчерашнего устного Тургора🫖
Задача. Дан треугольник 𝐴𝐵𝐶. Пусть 𝐶𝐿 — его биссектриса, 𝑊 — середина дуги 𝐵𝐶𝐴, а 𝑃 — проекция ортоцентра на медиану, проведённую из вершины 𝐶. Окружность 𝐶𝑃𝑊 пересекает прямую, проходящую через 𝐶 и параллельную 𝐴𝐵, в точке 𝑄. Докажите, что 𝐿𝐶 = 𝐿𝑄.
Ловите задачку со вчерашнего устного Тургора
Задача. Дан треугольник 𝐴𝐵𝐶. Пусть 𝐶𝐿 — его биссектриса, 𝑊 — середина дуги 𝐵𝐶𝐴, а 𝑃 — проекция ортоцентра на медиану, проведённую из вершины 𝐶. Окружность 𝐶𝑃𝑊 пересекает прямую, проходящую через 𝐶 и параллельную 𝐴𝐵, в точке 𝑄. Докажите, что 𝐿𝐶 = 𝐿𝑄.
Please open Telegram to view this post
VIEW IN TELEGRAM
#геом_разминка
Задача. Дан вписанный четырехугольник 𝐴𝐵𝐶𝐷. Пусть 𝐼 — центр вписанной окружности 𝐴𝐵𝐷, 𝐽 — центр вписанной окружности 𝐴𝐶𝐷. Перпендикуляр из точки 𝐼 на 𝐴𝐶 пересекается с перпендикуляром из точки 𝐽 на 𝐵𝐷 в точке 𝐾. Докажите, что 𝐼𝐾 = 𝐽𝐾.
Задача. Дан вписанный четырехугольник 𝐴𝐵𝐶𝐷. Пусть 𝐼 — центр вписанной окружности 𝐴𝐵𝐷, 𝐽 — центр вписанной окружности 𝐴𝐶𝐷. Перпендикуляр из точки 𝐼 на 𝐴𝐶 пересекается с перпендикуляром из точки 𝐽 на 𝐵𝐷 в точке 𝐾. Докажите, что 𝐼𝐾 = 𝐽𝐾.
#геом_разминка #кринж_недели
Задача. Точка 𝑃 лежит внутри остроугольного треугольника 𝐴𝐵𝐶. Точки 𝐷, 𝐸 и 𝐹 – основания перпендикуляров, опущенных из 𝑃 на стороны 𝐴𝐵𝐶. На шести отрезках, на которые эти точки разбивают стороны треугольника как на основаниях построены квадраты вне треугольника 𝐴𝐵𝐶. Эти квадраты попеременно раскрашены в красный и синий цвета. Рассмотрим два треугольника, образованных прямыми, содержащими «внешние» стороны квадратов одного цвета. Докажите, что эти треугольники равны.
Задача. Точка 𝑃 лежит внутри остроугольного треугольника 𝐴𝐵𝐶. Точки 𝐷, 𝐸 и 𝐹 – основания перпендикуляров, опущенных из 𝑃 на стороны 𝐴𝐵𝐶. На шести отрезках, на которые эти точки разбивают стороны треугольника как на основаниях построены квадраты вне треугольника 𝐴𝐵𝐶. Эти квадраты попеременно раскрашены в красный и синий цвета. Рассмотрим два треугольника, образованных прямыми, содержащими «внешние» стороны квадратов одного цвета. Докажите, что эти треугольники равны.
Как вы знаете, мы любим путешествовать ✈️
Каждый раз, когда мы оказываемся в новом городе 🌇 или стране, хотим поделиться с вами радостью открытий и геом находками 🔍
Мы запускаем новую рубрику #уголки_планеты 📐🌏, где будем публиковать задачи из путешествий и открыток :)
#геом_разминка спряталась на втором фото, как обычно ждем решения в комментах👇
Сегодня вспоминаем тульские пряники❤️
Каждый раз, когда мы оказываемся в новом городе 🌇 или стране, хотим поделиться с вами радостью открытий и геом находками 🔍
Мы запускаем новую рубрику #уголки_планеты 📐🌏, где будем публиковать задачи из путешествий и открыток :)
#геом_разминка спряталась на втором фото, как обычно ждем решения в комментах
Сегодня вспоминаем тульские пряники
Please open Telegram to view this post
VIEW IN TELEGRAM
Please open Telegram to view this post
VIEW IN TELEGRAM
#геом_разминка
Задача. Пусть 𝐶 — точка на полукруге диаметром 𝐴𝐵, а 𝐷 — середина дуги 𝐴𝐶. Пусть 𝐸 — проекция 𝐷 на прямую 𝐵𝐶, а 𝐹 — пересечение прямой 𝐴𝐸 с полукругом. Докажите, что 𝐵𝐹 делит пополам отрезок прямой 𝐷𝐸.
Задача. Пусть 𝐶 — точка на полукруге диаметром 𝐴𝐵, а 𝐷 — середина дуги 𝐴𝐶. Пусть 𝐸 — проекция 𝐷 на прямую 𝐵𝐶, а 𝐹 — пересечение прямой 𝐴𝐸 с полукругом. Докажите, что 𝐵𝐹 делит пополам отрезок прямой 𝐷𝐸.
#геом_разминка
Задача. Пусть 𝐴𝐵𝐶 — треугольник, а 𝐷 — основание высоты от точки 𝐴. Пусть 𝐸 и 𝐹 лежат на прямой, проходящей через 𝐷, так что 𝐴𝐸 перпендикулярна 𝐵𝐸, 𝐴𝐹 перпендикулярна 𝐶𝐹, а 𝐸 и 𝐹 отличаются от 𝐷. Пусть 𝑀 и 𝑁 —середины отрезков 𝐵𝐶 и 𝐸𝐹 соответственно. Докажите, что 𝐴𝑁 перпендикулярна 𝑁𝑀
Задача. Пусть 𝐴𝐵𝐶 — треугольник, а 𝐷 — основание высоты от точки 𝐴. Пусть 𝐸 и 𝐹 лежат на прямой, проходящей через 𝐷, так что 𝐴𝐸 перпендикулярна 𝐵𝐸, 𝐴𝐹 перпендикулярна 𝐶𝐹, а 𝐸 и 𝐹 отличаются от 𝐷. Пусть 𝑀 и 𝑁 —середины отрезков 𝐵𝐶 и 𝐸𝐹 соответственно. Докажите, что 𝐴𝑁 перпендикулярна 𝑁𝑀
Сможете ли вы бросить вызов компьютеру и одолеть бездушную машину 🤖
Суть игры:
▪️ до начала игры вы выбираете сторону за которую будете играть — Чётная или Нечётная (компьютер займёт противоположную)
▪️ в каждом раунде вы и компьютер независимо выбираете одно из двух чисел 1 или 2
▪️ итог по раунду определяется суммой выбранных чисел
Если сумма чётная (2, 4) → победа Чётной стороны!
Если сумма нечётная (1, 3) → победа Нечётной стороны!
В каждом раунде разыгрывается число монет, равное сумме выбранных чисел обеими сторонами. То есть если одна из сторон выбрала число 1, а вторая число 2, то выигрывает нечётная сторона и забирает 3=1+2 монеты. Чётная сторона теряет число монет, равное выбранному числу 🪙 Изначально у игроков по 200 монет.
Выигрывает сторона набравшая большее число монет по итогу игры, чем противник.
Мы проведем 100 раундов 🤯 Но мы не так жестоки чтобы заставить вас 100 раз выбирать какое то из двух чисел 1 или 2, поэтому мы сделаем это за вас 🙃
От вас мы ждем лишь одно число — вероятность с которой в каждом из раундов вы будете выбирать единицу.
Как это работает? 🤔
Объясним на примере. Скажем, вы выбрали Чётную сторону и вероятность 0.7. Это значит, что в каждом раунде вы будете играть за Чётного. При этом число которое вы назовете в этом раунде мы определим случайно: шанс что это будет 1 довольно высок — 0.7 по сравнению с шансом что эта будет двойка — 0.3.
То есть, выбрав вероятность 0.7 можно ожидать, что в среднем из 100 подбрасываний единица выпадет примерно 70 раз.
Переходите в нашего бота чтобы начать 👉 @bonka_game_eon_bot 👈
Игру завершим уже завтра в 22:00 🕙 Спешите!
P.S. Авторы провели ночь за моделированием... и теперь видят 1 и 2 даже в задачах по геоме, так что #кринж_недели гарантирован! 😵💫
Суть игры:
▪️ до начала игры вы выбираете сторону за которую будете играть — Чётная или Нечётная (компьютер займёт противоположную)
▪️ в каждом раунде вы и компьютер независимо выбираете одно из двух чисел 1 или 2
▪️ итог по раунду определяется суммой выбранных чисел
Если сумма чётная (2, 4) → победа Чётной стороны!
Если сумма нечётная (1, 3) → победа Нечётной стороны!
В каждом раунде разыгрывается число монет, равное сумме выбранных чисел обеими сторонами. То есть если одна из сторон выбрала число 1, а вторая число 2, то выигрывает нечётная сторона и забирает 3=1+2 монеты. Чётная сторона теряет число монет, равное выбранному числу 🪙 Изначально у игроков по 200 монет.
Выигрывает сторона набравшая большее число монет по итогу игры, чем противник.
Мы проведем 100 раундов 🤯 Но мы не так жестоки чтобы заставить вас 100 раз выбирать какое то из двух чисел 1 или 2, поэтому мы сделаем это за вас 🙃
От вас мы ждем лишь одно число — вероятность с которой в каждом из раундов вы будете выбирать единицу.
Как это работает? 🤔
Объясним на примере. Скажем, вы выбрали Чётную сторону и вероятность 0.7. Это значит, что в каждом раунде вы будете играть за Чётного. При этом число которое вы назовете в этом раунде мы определим случайно: шанс что это будет 1 довольно высок — 0.7 по сравнению с шансом что эта будет двойка — 0.3.
То есть, выбрав вероятность 0.7 можно ожидать, что в среднем из 100 подбрасываний единица выпадет примерно 70 раз.
Переходите в нашего бота чтобы начать 👉 @bonka_game_eon_bot 👈
Игру завершим уже завтра в 22:00 🕙 Спешите!
P.S. Авторы провели ночь за моделированием... и теперь видят 1 и 2 даже в задачах по геоме, так что #кринж_недели гарантирован! 😵💫
This media is not supported in your browser
VIEW IN TELEGRAM
#геом_разминка
Задача. Пусть 𝐷 — произвольная точка на стороне 𝐵𝐶 неравнобедренного остроугольного треугольника 𝐴𝐵𝐶. Окружность с центром 𝐷 и радиусом 𝐷𝐴 пересекает лучи 𝐴𝐵 (за точкой 𝐵) и 𝐴𝐶 (за точкой 𝐶) в точках 𝑀 и 𝑁. Докажите, что ортоцентр треугольника 𝐴𝑀𝑁 лежит на фиксированной прямой, независящей от выбора 𝐷.
Задача. Пусть 𝐷 — произвольная точка на стороне 𝐵𝐶 неравнобедренного остроугольного треугольника 𝐴𝐵𝐶. Окружность с центром 𝐷 и радиусом 𝐷𝐴 пересекает лучи 𝐴𝐵 (за точкой 𝐵) и 𝐴𝐶 (за точкой 𝐶) в точках 𝑀 и 𝑁. Докажите, что ортоцентр треугольника 𝐴𝑀𝑁 лежит на фиксированной прямой, независящей от выбора 𝐷.
#геом_разминка
Задача. Дан остроугольный треугольник 𝐴𝐵𝐶 (𝐴𝐵 < 𝐴𝐶) с центром описанной окружности 𝑂 и ортоцентром 𝐻. Касательная в точке 𝐴 к описанной окружности 𝐴𝐵𝐶 пересекает 𝐵𝐶 в точке 𝑇. Пусть 𝑋 — середина 𝐴𝐻. Докажите, что ∠𝐴𝑇𝑋 = ∠𝑂𝑇𝐵.
Задача. Дан остроугольный треугольник 𝐴𝐵𝐶 (𝐴𝐵 < 𝐴𝐶) с центром описанной окружности 𝑂 и ортоцентром 𝐻. Касательная в точке 𝐴 к описанной окружности 𝐴𝐵𝐶 пересекает 𝐵𝐶 в точке 𝑇. Пусть 𝑋 — середина 𝐴𝐻. Докажите, что ∠𝐴𝑇𝑋 = ∠𝑂𝑇𝐵.