#геом_разминка
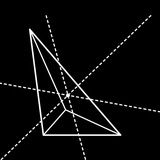
Задача. Каждая из сторон 𝐴𝐵 и 𝐶𝐷 выпуклого четырёхугольника 𝐴𝐵𝐶𝐷 разделена на три равные части, 𝐴𝐸 = 𝐸𝐹 = 𝐹𝐵, 𝐷𝑃 = 𝑃𝑄 = 𝑄𝐶. Диагонали 𝐴𝐸𝑃𝐷 и 𝐹𝐵𝐶𝑄 пересекаются в точках 𝑀 и 𝑁 соответственно. Докажите, что сумма площадей треугольников 𝐴𝑀𝐷 и 𝐵𝑁𝐶 равна сумме площадей треугольников 𝐸𝑃𝑀 и 𝐹𝑁𝑄.
Задача. Каждая из сторон 𝐴𝐵 и 𝐶𝐷 выпуклого четырёхугольника 𝐴𝐵𝐶𝐷 разделена на три равные части, 𝐴𝐸 = 𝐸𝐹 = 𝐹𝐵, 𝐷𝑃 = 𝑃𝑄 = 𝑄𝐶. Диагонали 𝐴𝐸𝑃𝐷 и 𝐹𝐵𝐶𝑄 пересекаются в точках 𝑀 и 𝑁 соответственно. Докажите, что сумма площадей треугольников 𝐴𝑀𝐷 и 𝐵𝑁𝐶 равна сумме площадей треугольников 𝐸𝑃𝑀 и 𝐹𝑁𝑄.
#геом_разминка
Задача. Пусть 𝐴𝐵𝐶 — прямоугольный треугольник с углом 𝐴 = 90°, точка 𝐷 — основание высоты из 𝐴 на 𝐵𝐶, а 𝐸 — средина 𝐷𝐶. Окружность 𝐴𝐵𝐷 вторично пересекает 𝐴𝐸 в точке 𝐹. Пусть 𝑋 — это пересечение прямых 𝐴𝐵 и 𝐷𝐹. Докажите, что 𝑋𝐷 = 𝑋𝐶.
Задача. Пусть 𝐴𝐵𝐶 — прямоугольный треугольник с углом 𝐴 = 90°, точка 𝐷 — основание высоты из 𝐴 на 𝐵𝐶, а 𝐸 — средина 𝐷𝐶. Окружность 𝐴𝐵𝐷 вторично пересекает 𝐴𝐸 в точке 𝐹. Пусть 𝑋 — это пересечение прямых 𝐴𝐵 и 𝐷𝐹. Докажите, что 𝑋𝐷 = 𝑋𝐶.
#геом_разминка
Угадайте где мы?📍
Задача. Пусть 𝐴𝐵𝐶 остроугольный треугольник, 𝑘 — его описанная окружность с центром 𝑂. Прямая, проходящая через 𝑂 пересекает стороны 𝐴𝐵 и 𝐴𝐶 в точках 𝐷 и 𝐸 соответственно. Пусть 𝐵′ и 𝐶′ — симметрии 𝐵 и 𝐶 относительно 𝑂 соответственно. Докажите, что (𝑂𝐷𝐶′) и (𝑂𝐸𝐵′) пересекаются на 𝑘.
Доброго утра и прекрасного настроения 🥰
Угадайте где мы?
Задача. Пусть 𝐴𝐵𝐶 остроугольный треугольник, 𝑘 — его описанная окружность с центром 𝑂. Прямая, проходящая через 𝑂 пересекает стороны 𝐴𝐵 и 𝐴𝐶 в точках 𝐷 и 𝐸 соответственно. Пусть 𝐵′ и 𝐶′ — симметрии 𝐵 и 𝐶 относительно 𝑂 соответственно. Докажите, что (𝑂𝐷𝐶′) и (𝑂𝐸𝐵′) пересекаются на 𝑘.
Доброго утра и прекрасного настроения 🥰
Please open Telegram to view this post
VIEW IN TELEGRAM