group-telegram.com/ad_research/401
Last Update:
#статистика_для_котиков
Эти интервалы не внушают доверия
Привет, коллега!
В прошлый раз мы говорили про стандартную ошибку среднего (SEM) и тех редких случаях, когда её всё же можно использовать для оценки разброса. Но даже если у тебя нет кучи выборок с n<30, а есть всего лишь одна, SEM можно использовать для расчёта доверительных интервалов для математического ожидания. Однако, у использования именно такого метода есть два ограничения: выборка должна быть достаточно большая (больше 30 значений) и дисперсия генеральной совокупности должна быть известна. Последний пункт в исследованиях выполняется редко, однако дисперсия очень большой выборки примерно равна дисперсии генеральной совокупности и эти два параметра сходятся
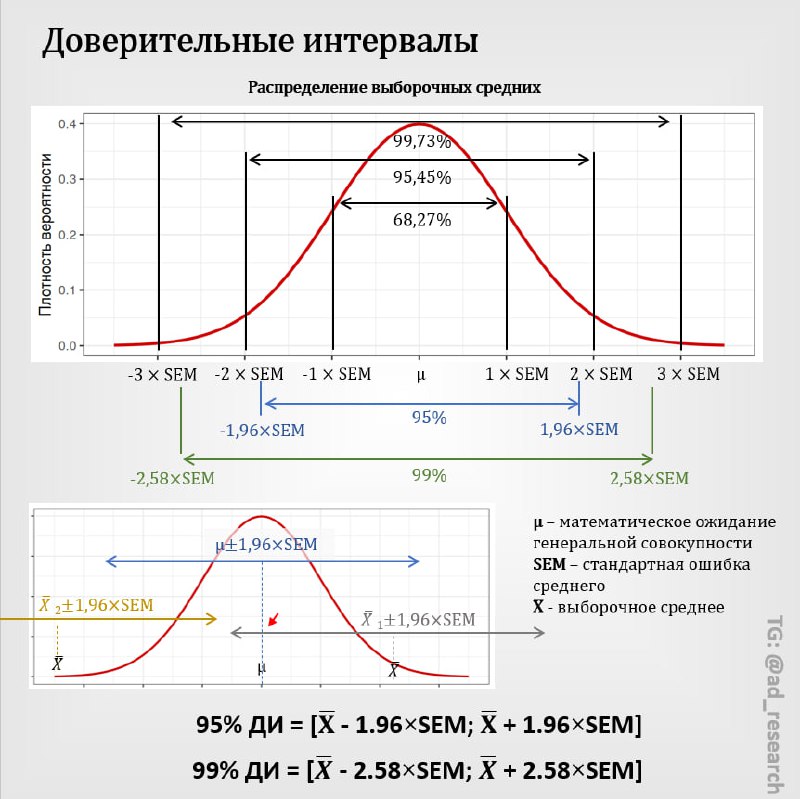
Итак, откуда же берутся доверительные интервалы. Вспомним сначала предыдущий пост: если из генеральной совокупности с количественными непрерывными данными, имеющей любое распределение, извлекать выборки размером n>30, то средние значения этих бесконечных выборок сформируют своё распределение, которое будет нормальным, его среднее будет равно математическому ожиданию генеральной совокупности (μ), а стандартное отклонение будет равно SEM (дисперсия генеральной совокупности, делённая на корень из количества значений выборки).
Теперь собственно будем в этом самом нормальном распределении выборочных средних существовать. Помнишь, я писала про замечательное свойство нормального распределения, именуемое "правилом трёх сигм"? Его тоже сейчас придётся вспомнить, а особенно тот факт, что 95,45% значений нормальной выборки лежат в пределах 2 стандартных отклонений (σ) от математического ожидания, а 99,73% в пределах трёх σ. Для нашего распределения выборочных средних σ это SEM.
Но все эти сотые доли после запятой - вещь не слишком удобная
Теперь смотри какая магия
UPD: То есть, если мы проведём бесконечное количество экспериментов и для каждого выборочного среднего постоим доверительный интервал, то в 95% случаев в этот интервал попадёт математическое ожидание генеральной совокупности. Изначально я дала иное определение, которое вызвало бурную реакцию в комментариях, поэтому приняла решение изменить пост. Однако общее определение любого доверительного интервала я оставлю: Доверительный интервал — это интервал, который строится на основе случайной выборки и содержит неизвестный параметр генеральной совокупности с заданной вероятностью.
В плане графического представления данных доверительные интервалы иногда лучше, чем различные меры разброса, так как они описывают не отдельную выборку, а уже касаются генеральной совокупности. Стоит отметить, что доверительные интервалы существуют и для разности средних, медианы, для долей, для пропорций, для регрессий и много чего ещё. И некоторые из них когда-нибудь получат свой отдельный пост.
Возможно сейчас я вдохновила тебя на использование доверительных интервалов в работе, но не забывай про ограничения, которое я упомянула в начале поста: как минимум выборка должна быть достаточно большой, а в идеале должна быть известна дисперсия генеральной совокупности