group-telegram.com/gepardchan/107
Last Update:
Объяснение формулы Байеса
Если вам нравятся длинные статьи, то можете почитать объяснение Юдковского на LessWrong или по этой ссылке (на английском). Ниже будет мое компактное изложение основных идей.
Рассмотрим следующую задачу:
> Пусть существует заболевание с частотой распространения среди населения 0,001 и метод диагностического обследования, который с вероятностью 0,9 выявляет больного, но при этом имеет вероятность 0,01 ложноположительного результата — ошибочного выявления заболевания у здорового человека. Найти вероятность того, что человек здоров, если он был признан больным при обследовании.
(Если вы никогда ранее не сталкивались с похожими задачами, то попробуйте сначала прикинуть ответ, а потом уже дочитать вниз и проверить свои догадки.)
Понятно, что можно решать ее, используя формулу Байеса напрямую (посчитать P(A), P(B), P(B|A) и из этого вывести ответ на задачу P(A|B)), но есть и более короткий путь.
Поскольку вероятность быть больным до теста равна 0.001, то получается, что шансы болезни изначально 1:999 (или отношение больных и здоровых равно 1/999). Далее нам требуется поделить вероятность true positive на вероятность false positive — получится 0.9/0.01 = 90. Наконец, умножаем 1/999 на 90 и получаем 90/999, или в переводе обратно в вероятность быть здоровым, 999/(90+999) ≈ 0.9174.
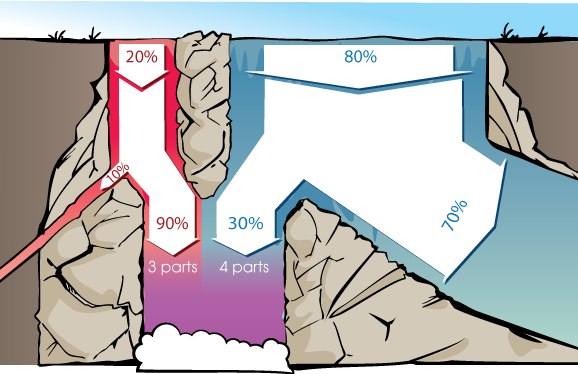
Строгое математическое доказательство остается в качестве упражнения читателю :) Но интуитивно это решение можно понимать с помощью водопада (картинка взята отсюда) На картинке синяя вода — это вероятность здорового, а красная — вероятность больного. Фиолетовая область — это то, что мы наблюдаем после теста: либо больного с положительным тестом, либо здорового с ложноположительным тестом. При этом доля обнаруженных случаев (true positive rate, TPR) — 90%, а ложноположительных срабатываний (false positive rate, FPR) — 30%. Тогда изначально отношение синей и красной воды было 80/20 = 4, а в фиолетовой области оно стало (80*30)/(20*90) = 4/3, т.е. разделилось на 90/30 = 3 — отношение TPR и FPR.
(продолжение ниже)
BY Гепардово гнездо
Share with your friend now:
group-telegram.com/gepardchan/107
