Математические байки
1999-1-circles-parabolas-markelov.pdf
Собственно, как Серёжа пишет в тексте «Circles and Parabolas», сначала он наткнулся на задачу в American Mathematical Monthly:
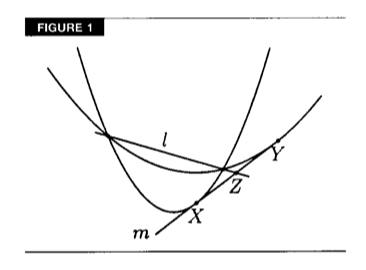
Задача. Пусть даны две пересекающиеся параболы с вертикальными осями. Тогда прямая, проходящая через две их точки пересечения, делит их отрезок их общей касательной, заключённый между точками касания, пополам (см. Figure 1).
И эта задача замечательно перекликается с известным (и доказывающимся, например, через степень точки) утверждением про окружности:
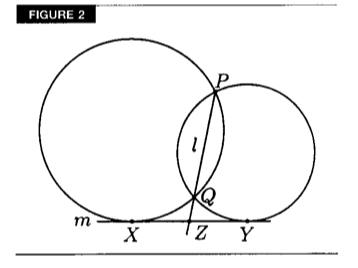
Задача. Пусть даны две пересекающиеся окружности. Тогда прямая, проходящая через две их точки пересечения, делит их отрезок их общей касательной, заключённый между точками касания, пополам (см. Figure 2).
===
Рисунки я взял из текста выше — S. Markelov, Circles and Parabolas, The Mathematical Intelligencer, 21 (1999). Кстати — этот текст вышел в колонке «Mathematical entertainment» под редакцией А. Шеня, и дальше в той же колонке идёт письмо В. В. Успенского про потрясающе красивое трёхмерное доказательство теоремы Брианшона — с использованием однополостного гиперболоида, двух семейств прямых на нём и «вида сверху». Я вот раньше не знал!
Задача. Пусть даны две пересекающиеся параболы с вертикальными осями. Тогда прямая, проходящая через две их точки пересечения, делит их отрезок их общей касательной, заключённый между точками касания, пополам (см. Figure 1).
И эта задача замечательно перекликается с известным (и доказывающимся, например, через степень точки) утверждением про окружности:
Задача. Пусть даны две пересекающиеся окружности. Тогда прямая, проходящая через две их точки пересечения, делит их отрезок их общей касательной, заключённый между точками касания, пополам (см. Figure 2).
===
Рисунки я взял из текста выше — S. Markelov, Circles and Parabolas, The Mathematical Intelligencer, 21 (1999). Кстати — этот текст вышел в колонке «Mathematical entertainment» под редакцией А. Шеня, и дальше в той же колонке идёт письмо В. В. Успенского про потрясающе красивое трёхмерное доказательство теоремы Брианшона — с использованием однополостного гиперболоида, двух семейств прямых на нём и «вида сверху». Я вот раньше не знал!
group-telegram.com/mathtabletalks/4614
Create:
Last Update:
Last Update:
Собственно, как Серёжа пишет в тексте «Circles and Parabolas», сначала он наткнулся на задачу в American Mathematical Monthly:
Задача. Пусть даны две пересекающиеся параболы с вертикальными осями. Тогда прямая, проходящая через две их точки пересечения, делит их отрезок их общей касательной, заключённый между точками касания, пополам (см. Figure 1).
И эта задача замечательно перекликается с известным (и доказывающимся, например, через степень точки) утверждением про окружности:
Задача. Пусть даны две пересекающиеся окружности. Тогда прямая, проходящая через две их точки пересечения, делит их отрезок их общей касательной, заключённый между точками касания, пополам (см. Figure 2).
===
Рисунки я взял из текста выше — S. Markelov, Circles and Parabolas, The Mathematical Intelligencer, 21 (1999). Кстати — этот текст вышел в колонке «Mathematical entertainment» под редакцией А. Шеня, и дальше в той же колонке идёт письмо В. В. Успенского про потрясающе красивое трёхмерное доказательство теоремы Брианшона — с использованием однополостного гиперболоида, двух семейств прямых на нём и «вида сверху». Я вот раньше не знал!
Задача. Пусть даны две пересекающиеся параболы с вертикальными осями. Тогда прямая, проходящая через две их точки пересечения, делит их отрезок их общей касательной, заключённый между точками касания, пополам (см. Figure 1).
И эта задача замечательно перекликается с известным (и доказывающимся, например, через степень точки) утверждением про окружности:
Задача. Пусть даны две пересекающиеся окружности. Тогда прямая, проходящая через две их точки пересечения, делит их отрезок их общей касательной, заключённый между точками касания, пополам (см. Figure 2).
===
Рисунки я взял из текста выше — S. Markelov, Circles and Parabolas, The Mathematical Intelligencer, 21 (1999). Кстати — этот текст вышел в колонке «Mathematical entertainment» под редакцией А. Шеня, и дальше в той же колонке идёт письмо В. В. Успенского про потрясающе красивое трёхмерное доказательство теоремы Брианшона — с использованием однополостного гиперболоида, двух семейств прямых на нём и «вида сверху». Я вот раньше не знал!
BY Математические байки
Share with your friend now:
group-telegram.com/mathtabletalks/4614
