Forwarded from Геометрия от Волчкевича
Верю — не верю
Некоторые из приведенных ниже шести утверждений верны в общем случае. Какие?
Некоторые из приведенных ниже шести утверждений верны в общем случае. Какие?
Anonymous Poll
49%
1. Если у двух четырехугольников совпадают все 4 вершины, то они имеют равные площади.
51%
2. В геометрии Лобачевского для любого треугольника есть прямая, равноудалённая от всех его вершин.
42%
3. Центр окружности, вписанной в египетский треугольник, равноудален от середин двух его сторон.
41%
. Если р/б треугольник можно разрезать на три меньших р/б треугольника, то два из них равны.
39%
5. Если прямая делит пополам площадь 4-угольника и 2 его стороны, то он параллелограмм или трапеция.
46%
6. Если все вершины многогранника лежат на одной сфере, то этот многогранник выпуклый.
Forwarded from JustScience | Олимпиадная Математика
#геометрия #задача
Прямая, проходящая через ортоцентр треугольника ABC пересекает его стороны AB и AC в точках D и E соответственно. Сторона BC, перпендикуляр к AB в точке D и перпендикуляр к AC в точке E образуют треугольник T. Докажите, что описанные окружности треугольников T и ABC касаются.
Прямая, проходящая через ортоцентр треугольника ABC пересекает его стороны AB и AC в точках D и E соответственно. Сторона BC, перпендикуляр к AB в точке D и перпендикуляр к AC в точке E образуют треугольник T. Докажите, что описанные окружности треугольников T и ABC касаются.
Замкнутая четырехзвенная ломаная описана вокруг сферы. Доказать, что точки касания лежат в одной плоскости.
// П.Пушкарь напомнил такую задачу с ММО-1950
// П.Пушкарь напомнил такую задачу с ММО-1950
а) Пусть 4 окружности на плоскости касаются друг друга по циклу (внешним образом). Доказать, что точки касания лежат на одной окружности.
б) То же не на плоскости, а на сфере.
в) Вывести отсюда предыдущую задачу.
// по мотивам обсуждения в комментариях
б) То же не на плоскости, а на сфере.
в) Вывести отсюда предыдущую задачу.
// по мотивам обсуждения в комментариях
Forwarded from Фулл и точка
#геом_разминка
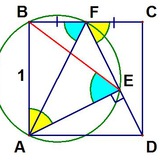
Задача. Внутри квадрата 𝐴𝐵𝐶𝐷 взята точка 𝑃 такая, что 𝐴𝑃 : 𝐵𝑃 : 𝐶𝑃 = 1 : 2 : 3. Найдите угол 𝐴𝑃𝐵.
Пусть никакие трудности вас не пошатнут 🗿
Задача. Внутри квадрата 𝐴𝐵𝐶𝐷 взята точка 𝑃 такая, что 𝐴𝑃 : 𝐵𝑃 : 𝐶𝑃 = 1 : 2 : 3. Найдите угол 𝐴𝑃𝐵.
Пусть никакие трудности вас не пошатнут 🗿
2024-09-markelov-zaslavsky.pdf
503.6 KB
статья А.Заславского и С.Маркелова «Трисекция угла и другие классические задачи» (Квант №9 за 2024 год)
обсуждается трисекция с помощью коник и проч., по мотивам проекта на ЛКТГ
обсуждается трисекция с помощью коник и проч., по мотивам проекта на ЛКТГ
Forwarded from Геометрия с Ниловым
Два разных замощения плоскости (спиралевидное и кольцеобразное) копиями многоугольника, изображенного сверху, из книги Грюнбаума и Шепарда "Замощения и орнаменты"
Forwarded from Олимпиадная геометрия
Эта замечательная задача давно стала классикой — выдал ее на занятии на этой неделе. Весной этой задаче исполнится 30 лет.
Ее автор Сергей Маркелов, замечательный человек, которого сегодня увы не стало.
Ее автор Сергей Маркелов, замечательный человек, которого сегодня увы не стало.
1999-1-circles-parabolas-markelov.pdf
1.6 MB
S.Markelov. Circles and parabolas
// А.Акопян пишет: «В книжке с картинками есть целая серия задач про параболы, для которых выполняются классические теоремы про окружности. Мало кто знает, но этот трюк обнаружил Серёжа. Сейчас это уже является базой для продвинутых олимпиадных геометров, но тогда это было полной неожиданностью.»
// А.Акопян пишет: «В книжке с картинками есть целая серия задач про параболы, для которых выполняются классические теоремы про окружности. Мало кто знает, но этот трюк обнаружил Серёжа. Сейчас это уже является базой для продвинутых олимпиадных геометров, но тогда это было полной неожиданностью.»
Forwarded from Геометрия с Ниловым
razr-itog.pdf
135.4 KB
Вчера не стало Сергея Маркелова. Соболезнования близким 🙏
Forwarded from Фулл и точка
#красота_спасет_мир
Подошла к концу олимпиада ЮМШ 🥇 Публикуем задачку, которая предлагалась в девятом классе 🔥
Задача. Дан вписанный выпуклый четырёхугольник 𝐴𝐵𝐶𝐷. Точки 𝑃, 𝑄, 𝑅, 𝑆 выбраны на прямых 𝐴𝐷, 𝐴𝐵, 𝐶𝐵, 𝐷𝐶 так, что 𝑃𝑄 ⊥ 𝐴𝐵, 𝑄𝑅 ⊥ 𝐵𝐶, 𝑅𝑆 ⊥ 𝐶𝐷 и 𝑆𝑃 ⊥ 𝐷𝐴. Оказалось, что четырёхугольники 𝑃𝑄𝑅𝑆 и 𝐴𝐵𝐶𝐷 (соответственно) подобны. Докажите, что центр описанной окружности четырёхугольника 𝑃𝑄𝑅𝑆 — это точка пересечения диагоналей 𝐴𝐵𝐶𝐷.
Подошла к концу олимпиада ЮМШ 🥇 Публикуем задачку, которая предлагалась в девятом классе 🔥
Задача. Дан вписанный выпуклый четырёхугольник 𝐴𝐵𝐶𝐷. Точки 𝑃, 𝑄, 𝑅, 𝑆 выбраны на прямых 𝐴𝐷, 𝐴𝐵, 𝐶𝐵, 𝐷𝐶 так, что 𝑃𝑄 ⊥ 𝐴𝐵, 𝑄𝑅 ⊥ 𝐵𝐶, 𝑅𝑆 ⊥ 𝐶𝐷 и 𝑆𝑃 ⊥ 𝐷𝐴. Оказалось, что четырёхугольники 𝑃𝑄𝑅𝑆 и 𝐴𝐵𝐶𝐷 (соответственно) подобны. Докажите, что центр описанной окружности четырёхугольника 𝑃𝑄𝑅𝑆 — это точка пересечения диагоналей 𝐴𝐵𝐶𝐷.
Forwarded from Олимпиадная геометрия
Forwarded from Геометрия с Ниловым
Можно ли в плоскости прорезать тонкое отверстие, не разбивающее ее на части, через которое можно продеть каркас: a) куба; b) тетраэдра? (Ребра каркаса считаются сколь угодно тонкими)